Introducción al Análisis de Circuitos AC: Senoides, Vesores y Fasores.

Senoides

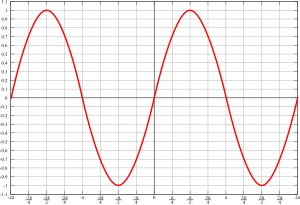
    Una Senoide o Sinusoide es la representación gráfica de la función Seno, es una función que representa una ondulación y es similar a la función del coseno, la cual se considera también una función sinusoidal. Dichas funciones pueden presentar al voltaje "V(t)" o a la corriente "I(t)" dada la función:

X(wt)=Xm*sen(wt)

    Donde:

• X(wt); puede representar a V(t) y I(t).
• Xm; es el valor pico de la función sinusoidal; es decir, el valor máximo.
• w; es la frecuencia angular en radianes del sistema.

    Los senoides también son funciones periódicas por lo que existe un periodo "T" que es el tiempo que dura la función en su recorrido hasta que vuelva a repetirse; por lo que si existe un periodo, debe existir una frecuencia que mide las veces que la señal cambia durante un periodo; por lo que:

f=1/T  ;    wT=2π   ;    w=2π/T=2πf

    En la existencia de dos funciones senoidales, estas pueden estar desfasadas unas de otras. Eso significa que tomando una función de referencia, la segunda función esta desplazada a la izquierda o a la derecha. Matemáticamente esto se demuestra de la siguiente manera:

    Dadas las siguientes funciones:

X1(t)=Xm1*sen(wt)

X2(t)=Xm2*sen(wt+𝝷)

    Donde:

• 𝝷; es el ángulo de fase.

    En este caso la función X1(t) esta retrasada 𝝷 con respecto a X2(t).

Versores y Fasores

     Un versor es un vector giratorio de módulo igual a la unidad que se represente como: e^(jwt), donde:

• w; representa la velocidad angular de rotación.

    El producto de la magnitud de un vector por un versor, convierte al producto en un vector giratorio.

A*e^(jwt)=|A|*e^(j(wt+𝝷))

    Dichos vectores giratorios tienen parte real y parte imaginaria; por lo que e un número complejo:

REAL|A|=|A|cos(wt+𝝷)

IMAG|A|=|A|sen(wt+𝝷)

    Estos fasores representan las transformadas vectoriales del voltaje y de la corriente, dado que "i(t)" pasa a ser el fasor de I y "v(t)" pasa a ser el fasor de V.