Introducción a Circuito RLC: Ecuaciones Diferenciales

    Las ecuaciones diferenciales son ecuaciones que contienen derivadas de una o más variables con respecto a una o más variables independientes. Se denomina una solución de la ecuación en el intervalo a cualquier función f(), definida en un intervalo "I", que tiene al menos "n" derivadas continuas de "I", las cuales cuando se sustituyen en una ecuación diferencial ordinaria de n-ésimo orden, reducen la ecuación a una identidad.

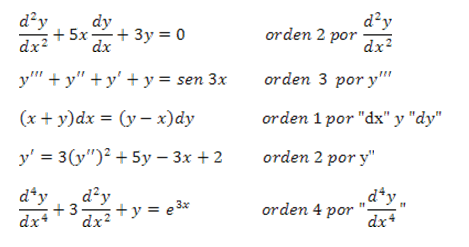
    Clasificación de Ecuaciones Diferenciales:

Tipo

• Ordinarias (EDO).
• Parciales (EDP).

Orden: Está determinado por la derivada de mayor orden de la ecuación diferencial.

Grado: Grado de la derivada de mayor orden de la ecuación diferencial.

Linealidad: Una EDO es lineal si cumple con las siguientes condiciones.

• La función incógnita y sus derivadas están en primer grado en la ecuación diferencial.
• Los coeficientes de la ecuación y la función a la que se igualan los términos que contienen a la función incógnita y sus derivadas, sean a lo más, funciones de la(s) variable(s) independiente(s).

Homogeneidad:

• Si la función a la que se iguala la ecuación diferencial; llámese "g(x)", es igual a 0, la diferencial es homogénea. 
• Si la función g(x) es distinta a 0, la diferencial es "No Homogénea".