Leyes de Kirchhoff: División de Voltaje y División de Corriente

    Gustav Kirchhoff fue un físico alemán del siglo XIX que hizo un gran avance en el rama de la electricidad con dos simples leyes que permitieron el estudio de mallas y de nodos. Las mallas no son más que una trayectoria cerrada en un circuito eléctrico que contiene elementos pasivos y/o activos y un nodo es un punto en el cual dos o más elementos tienen una conexión en común. 

    La primera ley de este fisico alemán se conoce como "La Ley de Corrientes de Kirchhoff" y dice:

La suma algebraica de las corrientes que entran a cualquier nodo es igual a cero. Kirchhoff

 

    Esta ley abre paso al estudio de nodos diciendo que la suma de TODAS las corrientes que entran o salen de un nodo son igual a 0 (Revisar el libro de Hayt o de Floyd para mejor ilustración) a esto se debe acordar que la corriente es la relación entre el voltaje y la resistencia.

    La segunda ley se conoce como "La Ley de Tensión de Kirchhoff", esta menciona que:

La suma algebraica de las tensiones alrededor de cualquier trayectoria cerrada es cero. Kirchhoff

    Esta ley permite el estudio de mallas de un circuito eléctrico. Se debe tomar en cuenta que el voltaje es la relación de la corriente por su resistencia eléctrica. 

   En la entrada de arreglos de resistencias vimos que cuando las resistencias están en paralelo, el voltaje de entrada es igual a la suma de los voltajes en las resistencias del circuito. Gracias a la ley de kirchhoff se comprueba esta teoria; ya que la sumatoria de todos los voltajes del circuito debe ser igual a 0, por lo tanto:

Vt-VR1-VR2=0     ;       Vt=VR1+VR2

    Como la corriente es la misma cuando las resistencias están en series se puede aplicar la siguiente propiedad. El voltaje deseado será igual al voltaje total por la resistencia del voltaje deseado entre la sumatoria de las resistencias. Eso se puede demostrar de la siguiente manera:

i=V/(R1+R2)   ;     Se multiplica por R2

i*R2=V*R2/(R1+R2)

i*R2=VR2

VR2=V*R2/(R1+R2)

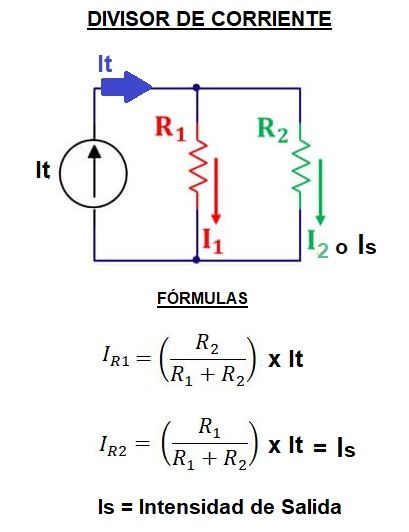
    De la misma forma, debido a Kirchhoff sabemos que i-i1-i2=0; por lo que i=i1+i2. Entonces tambien se puede realizar una división de corriente. Se  puede demostrar de la siguiente manera

1/Rt=(1/R1)+(1/R2)

RT=(R1*R2)/(R1+R2)

V=R1*R2*it/(R1+R2)

V/R1=R1*R2*it/(R1+R2)*R1

V/R1=i1

i1=R2*it/(R1+R2)

    Por lo que podemos observar que la corriente deseada será la multiplicación de la corriente total en por la resistencia opuesta entre la sumatoria de las resistencias.